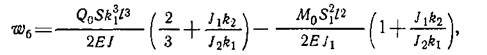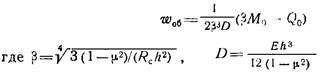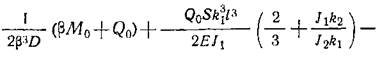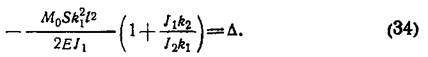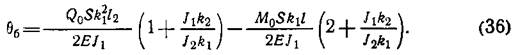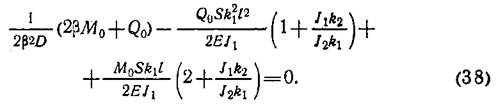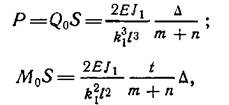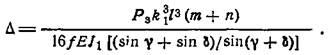Рулевое управление автомобилем и безопасность конструкции — Часть 16: Схема для расчета усилия осевого смещения шлицевого вала рулевого управления с энергопоглощающим элементом телескопирующего типа

Сила контактного давления определяется из условия совместности деформации втулки и вала в точках их контактирования. Это условие будет следующим:

Где W_Н и W_В — радиальные перемещения точек соответственно втулки и вала в месте их контактирования; Δ — радиальный натяг в шлицевом соединении.

Жесткость вала значительно больше жесткости втулки, поэтому можно с достаточной для практических целей точностью считать, что |W_В|=0. Тогда условие (31) примет вид:

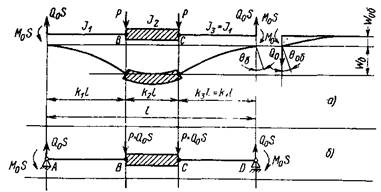
При определении радиальных перемещений во втулке каждая ее перемычка (рис. 57) рассматривается как балка переменного сечения, состыкованная в левом и правом сечениях I—I и VI—VI с цилиндрическими оболочками и нагруженная в точках Б и С сосредоточенными силами Р. Тогда:

Где ω_Об — радиальное перемещение цилиндрической оболочки в крайнем сечении; ω_Б — прогиб балки в точках В и С.

Рис. 57. Схема для расчета усилия осевого смещения шлицевого вала.

При определении ω_Об цилиндрическая часть втулки рассматривается как полубесконечная оболочка, нагруженная в крайнем сечении распределенными по длине окружности силами Q₀ и моментами М_Д.

При нахождении ω_Б перемычка рассматривается как балка переменного сечения, шарнирно закрепленная по краям и нагруженная силами P, моментами M_OS и силами Q_OS. В данном случае S=0,5πR_С (где R_C — средний радиус оболочки).

Пользуясь методом Мора, определим прогиб балки ω_Б в сечениях B и B:

Где l — длина прорези на втулке; k₁ k₂ и k₃—коэффициенты, определяющие длины шлицованной и гладкой частей прорези; J₁ и J₂ — моменты инерции секторов соответственно сечений II—II и III—III.

Радиальное перемещение цилиндрической оболочки:

– цилиндрическая жесткость оболочки (E — модуль упругости; h — толщина оболочки; μ — коэффициент Пуассона).

Найденные значения ω_Об и ω_Б позволяют определить ω_И. Подставив ω_Н в уравнение (33), получим:

Это уравнение содержит два неизвестных М₀ и Q₀. Для их определения необходимо составить еще одно уравнение, приравняв углы поворота крайних сечений балки А и D углу поворота конечного сечения оболочки, получим недостающее уравнение:

Пользуясь также методом Мора, найдем:

Угол поворота сечения оболочки определим по формуле:

Подставляя выражения (36) и (37) в уравнение (35), получим:

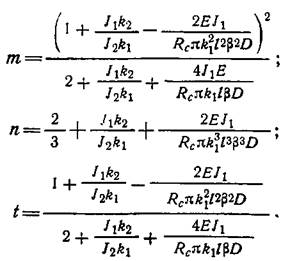
Решая совместно систему уравнений (34) и (38) и учитывая, что S=0,5πR, получим:

Где:

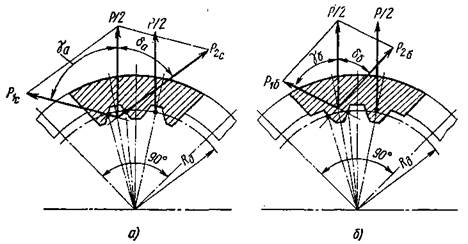
В связи с тем, что при нарезании шлицев во втулке протяжка не ориентируется по отношению к перемычкам, зубья шлицев могут располагаться в различных угловых положениях по отношению к средней продольной плоскости перемычки (балки). На рис. 58 показаны возможные крайние варианты расположения зубьев шлицев. Подсчитанное значение P связано с величиной P_{д. с}, входящей в формулу для определения усилия запрессовки, следующим выражением:

Рис. 58. Крайние варианты расположения зубьев шлицев.

При конструкторских разработках, задавая усилие запрессовки (сдвига) и назначая размеры вала и втулки, можно найти требуемый радиальный натяг:

Все части: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16

Купить цветные линзы illusion colors elegance Glavlinza.