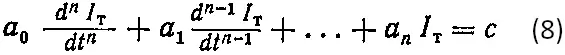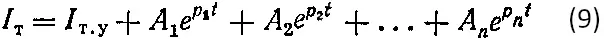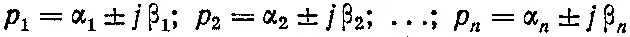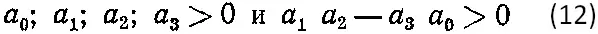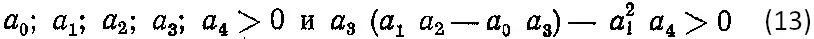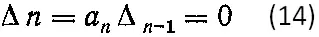Непосредственное суждение по вопросу электрической устойчивости и качества переходных процессов может быть получено в результате составления дифференциальных уравнений всех исследуемых контуров и анализа корней характеристического уравнения. Для проверки качества переходных процессов при уравнениях не свыше второго и третьего порядков построение кривых переходного процесса часто выполняют на основе исходных дифференциальных уравнений.
В результате совместного решения уравнений контуров получается уравнение высшего порядка относительно переменного параметра одного из контуров, например, тока в цепи якоря электродвигателя троллейбуса.
Общее линейное дифференциальные уравнение может, например, иметь вид:
где n — порядок высшей производной (порядок уравнения);
a0, a1, …, an, c — постоянные коэффициенты.
Общее решение этого уравнения:
где Iт.у — установившееся значение тока в контуре при t → ∞;
A1, A2, …, An — постоянные коэффициенты;
p1, p2, …, pn — корни уравнения, в общем случае комплексные:
Эти корни находят из характеристического уравнения, в котором производные уравнения (8) заменяются степенными функциями, а правая часть приравнивается нулю, т. е.:
Для обеспечения электрической устойчивости необходимо, чтобы переменные составляющие правой части уравнения (9) стремились к нулю при t → ∞, т. е. I → Iт.у. Для этого достаточно, чтобы вещественные части всех корней (p1, p2, …, pn) были отрицательные, т. е. α1, α2, …, αn < 0.
У дифференциальных уравнений третьего и более высоких порядков определение корней характеристического уравнения требует весьма большой расчетной работы. В этом случае исследование целесообразно проводить или при помощи вычислительной машины, или пользоваться косвенными методами, позволяющими произвести оценку электрической устойчивости и переходных процессов без нахождения корней характеристического уравнения.
Методы оценки устойчивости по различным критериям и исследование качества переходных процессов изложены в литературе по автоматическому регулированию. Для уравнений со степенью не выше четвертого порядка наиболее удобным для оценки устойчивости является критерий Гурвица.
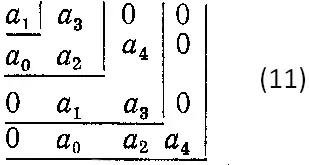
Критерий записывается в виде таблицы Гурвица, состоящей из n столбцов и строк, где n — степень дифференциального уравнения. Первая строка образуется из коэффициентов характеристического уравнения с нечетными индексами, начиная с a1 вторая строка — из коэффициентов с четными индексами, начиная с a0. Далее строки записываются в том же порядке так, чтобы по диагонали таблицы расположились коэффициенты в последовательности a1, a2, a3, …, an. Места коэффициентов с индексами меньше a0 и больше an заменяются нулями. Например, таблица Гурвица для уравнения четвертого порядка запишется так:
Из этой таблицы составляются очерченные прямыми определители Гурвица. Критерий устойчивости формулируется следующим образом.
Система устойчива, если a0 > 0 и все определители Гурвица больше нуля. Отсюда необходимым условием устойчивости является то, чтобы все коэффициенты характеристического уравнения были положительные.
Для уравнений первого и второго порядков этого условия достаточна для обеспечения устойчивости.
Для уравнения третьего порядка устойчивость обеспечивается при:
а для уравнения четвертого порядка:
Схема будет на границе устойчивости, когда высший определитель Гурвица равен нулю:
При an = 0 один из корней характеристического уравнения равен нулю (система находится на грани апериодической устойчивости).
При равенстве нулю определителя (Δn–1 = 0) два сопряженных корня характеристического уравнения находятся на мнимой оси (система находится на грани колебательной устойчивости).