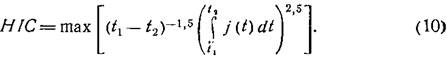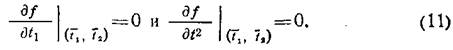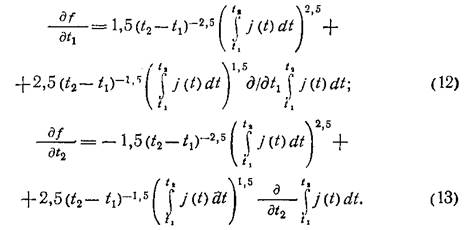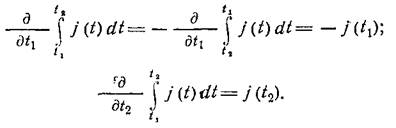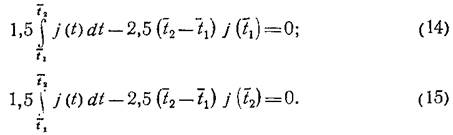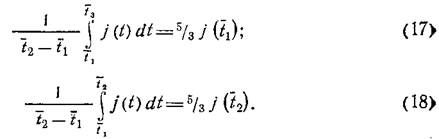Простой ударный импульс определяется аналитической функцией и характеризуется двумя независимыми параметрами: периодом воздействия по времени и амплитудой. Известная функция j(t) является непрерывной и интегрируемой в диапазоне где tΣ — полное время действия ударного импульса. Пределы интегрирования, переменные t1 и t2 критерия HIC должны находиться в этом же диапазоне:
Выражение (8) для HIC может быть записано в форме:
Правую часть выражения (10) рассматриваем как дифференцируемую функцию двух независимых переменных:
Функция двух переменных имеет экстремальное значение в некоторой точке (t1, t2) внутри исследуемого интервала если в этой точке будут равны нулю ее первые частные производные:
Условия (11) являются необходимыми, но недостаточными для существования экстремального значения в точке (t1, t2). Выполнение условий (11) означает лишь существование так называемой критической точки (может быть «седловина», а не максимум). Чтобы критическая точка оказалась экстремальной, необходимо исследовать поведение второй производной в окрестности этой точки.
Определим первые частные производные относительно t1 и t2:
В выражения (12) и (13) входят производные от интеграла по переменному верхнему (нижнему) пределу. Согласно теореме Ньютона — Лейбница, соответствующее значение производной равно значению подынтегральной функции на этом пределе. Отсюда имеем:
Упрощая выражения (12) и (13) и приравнивая их нулю, получим:
Система уравнений (14), (15) с двумя неизвестными t1 и t2 теоретически может быть решена, если известно аналитическое выражение подынтегральной функции j(tΣ), и ее первообразная функция позволит разрешить уравнения относительно неизвестных t1 и t2, не прибегая к численным методам.
Даже не имея конечного решения, из уравнений (14), (15) могут быть получены полезные результаты. Так, вычитая (14) из (15), имеем в критической точке (t1, t2)
Для нетривиального решения t2≠t1 в критической точке выполняется условие:
Равенство (16) показывает, что временной интервал, внутр, и которого критерий HIC достигает экстремального значения, располагается в окрестности вершины, границы этого интервала лежат на восходящей и нисходящей ветвях кривой замедления j(t), причем замедления на концах интервала равны.
Уравнения (14) и (15) можно представить в виде:
Принимая во внимание, что левые части уравнений (17) и (18) представляют собой средние значения ускорений в интервале t1<t<t2, а сами уравнения справедливы лишь при условии:
Т. е. t1 и 12 являются в данном случае найденными пределами интегрирования, может быть получен второй важный практический результат — среднее значение ускорения в пределах интегрирования t1<t<t2 равно значению ускорения в точке t1 (или t2), умноженному на 5/3.
Поскольку эти результаты позволяют значительно снизить число пар t1 и t2 для поиска пределов интегрирования, при которых HIC достигает максимума, они были положены в основу алгоритма для программы точного вычисления HIC по экспериментально найденной функции замедления головы манекена в процессе удара.
Единственное требование, которое предъявляется к этой функции для реализации указанной программы на ЭЦВМ, является ее непрерывность.
Для алгоритма и программы расчета на ЭЦВМ критерия HIC используем один из выводов, полученных для простого ударного импульса с одним экстремальным значением замедления, а именно — интервал по времени, в котором критерий HIC достигает максимального значения, начальное значение t1 располагается на восходящей, а конечное t2 — на нисходящей ветвях кривой замедления.