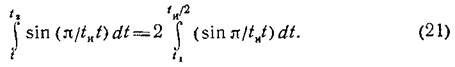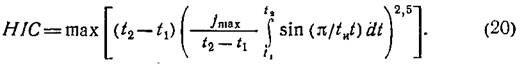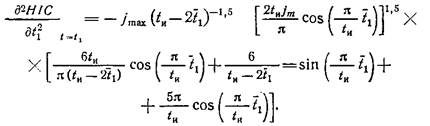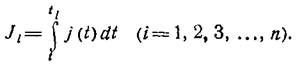Полученные результаты полезны также для экспресс-оценок уровня безопасности автомобилей, когда не требуется точного определения HIC, поскольку сравнительные оценки в этом случае могут быть осуществлены приближенно без использования вычислительной техники. Поиск вписанного в экспериментально полученную кривую j(t) прямоугольника, площадь которого максимальна, облегчит определение аргументов t1 и t2 для пределов интегрирования и может послужить в этом случае удобным практическим приемом.
Синусоидальный ударный импульс описывается уравнением:
Где tИ — продолжительность импульса; jMax—максимальное значение замедлений в частях g.
Описываемая кривая синусоидального ударного импульса симметрична относительно t = tи/2, поэтому из условия экстремума критерия HIC (16) задачу можно свести к одной действительной переменной, например, t1.
Из условий экстремума и симметрии имеем:
Из условия симметрии кривой замедления следует:
Относительно переменной t1 которая изменяется в интервале 0<t1<tи/2, определив функцию HIC для синусоидального импульса, используя выражение (8):
После интегрирования выражения (20) с использованием формул (19) и (21) получим уравнение для HIC в зависимости от одной независимой переменной t1:
После введения новой переменной μ=π(1/2—t1/tи) в уравнение (23) приходим к трансцендентному уравнению относительно μ:
Чтобы найти экстремальное значение HIC, необходимо продифференцировать по t1 правую часть уравнения (22) и выражение для первой производной приравнять нулю. После соответствующих преобразований для нетривиального решения t1<tи/2 получим:
С помощью численного метода определяются корень этого уравнения μ=0,33488, соответственно искомый параметр t1=0,16512 и подсчитывается значение HIC=0,4146tиJм2,5. Уравнение (23) определяет точку максимума, так как значение второй производной по t1 функции HIC в точке t1 отрицательно:
Решение критерия HIC для синусоидального ударного импульса может иметь практическое применение для экспресс-оценки критерия HIC по результатам исследований защитных удерживающих систем с антропоморфными манекенами. Если экспериментальную результирующую кривую 1 замедления головы манекена в период ударного воздействия можно аппроксимировать синусоидальным импульсом (рис. 44, б в части 1), то по двум параметрам tи и jmax подсчитывается критерий HIC:
Где kJ — коэффициент, зависящий от jmax.
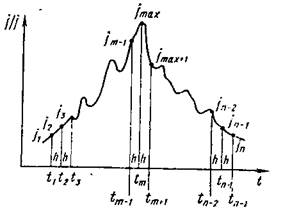
Рис. 45. Экспериментальная кривая замедлений головы манекена для формирования табличных значений.
Алгоритм расчета численного значения критерия HIC. Расчетное определение критерия HIC для экспериментальных кривых замедлений, которые имеют. непростую форму и несколько локальных экстремальных значений, возможно только с использованием численных методов.
Задача сводится к нахождению значений параметров t1 и t2, определяющих область максимизации функции HIC.
Пусть известна (рис. 45) экспериментальная результирующая кривая замедления j(t). Численный метод предполагает табличное задание исходной функции j(t). Выбирая постоянный шаг во времени h, формируем таблицу значений j(ti), каждому из которых присваивается индекс, изменяющийся от 1 до n.
Вычислим вектор значений интегралов:
Для исходной таблицы значений функции j(ti), заданной в равноотстоящих точках, ti = t1 + (i—1)h (i = 1, 2, 3, …, n).
Предполагается, что непрерывна интегрируемая функция j(t) и дважды дифференцируема. Начиная со значения интеграла J1=0, последовательно вычисляются все значения интеграла:
Максимальным значением замедления jMax (соответственно tMax) область значений аргумента разделяется на два участка. Согласно результатам исследования функции HIC для простого ударного импульса, область определения параметра t1 располагается в пределах первого участка (t1<t1<tmax) область определения параметра t2— в пределах второго участка (tmax<t2<tn). Используя вычисленный вектор значений интегралов JI(i = 1, 2, …, n), определяем значение HIC как максимум выражения: