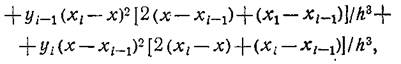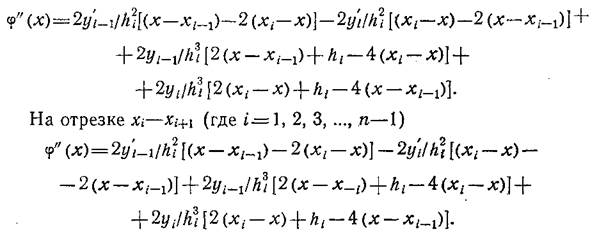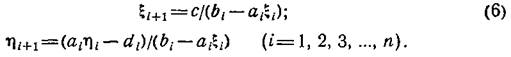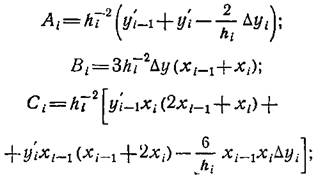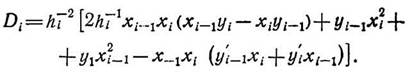Описание ветрового стекла при определении безопасности автомобиля

При описании исходных данных, характеризующих поверхность ветрового стекла, необходимо представить их как последовательность координат точек или, использовать аналитическое представление поверхности и границ стекла. Часто априори трудно выбрать удовлетворительный метод аппроксимации, поэтому целесообразен метод наиболее экономный в отношении ручной подготовки исходных данных для ЭЦВМ. В этом случае необходимо эффективно использовать доступную информацию, представленную в виде чертежей с проекциями ветрового стекла.

При всем многообразии ветровых стекол легковых автомобилей можно отметить их общие черты: стекло симметрично относительно продольной вертикальной плоскости автомобиля, проекции кромок и линии средней кривизны стекла с достаточной степенью точности могут быть описаны с помощью кубических сплайнов. Метод приближения и сглаживания исходных кривых на основе сплайн — аппроксимации позволяет свести к минимуму объем входной информации.

Кубическим сплайном называется функция ф(х), соединяющая N точек: х₁ х₂, х₃, х_N, имеет на заданном участке (х₁, x_N) непрерывные первую и вторую производные и на отрезках (x_i, x_i+1) равна многочлену третьей степени.

Кубический сплайн с коэффициентами кубического полинома A, B, C и D:

Этот сплайн обеспечивает совпадение с исходной функцией, а также непрерывность 1-й и 2-й производных в заданных точках соединения. Коэффициенты кубического полинома (1) на отрезке (x_i, x_i+1) однозначно определяются, если на его концах известны значения функции и ее первых производных. Используя для монотонного аргумента x_i<x_i+1 интерполяционную формулу Эрмита, которая требует, чтобы в узлах интерполяции совпадали значения не только функции, но и ее 1-й производной, можно записать два отрезка (x_i-1, x_i) (где i= 1, 2, …, n-1):

Где y — текущая ордината точек ветрового стекла; h=x_i—x_i+1, x_i-1≤x≤x_i.

Из условий сплайна можно получить равенство вторых производных в каждой внутренней узловой точке:

Аналогично можно написать интерполяционный многочлен Эрмита для отрезка x_i—x_i+1. Полагая Δy=y_i—y_i-1 и Δy_i+1=y_i+1—y_i и дифференцируя дважды ф(x), получим на отрезке x_i-1—x_i (где i=2, 3,…, n-1)

Где ф"(x_i^—) — вторая производная для i-го узла, вычисленная на отрезке x_i-1—x_i; ф"(x_i⁺) — вторая производная для i-ro узла, вычисленная на отрезке x_i—x_i+1.

Приравнивая значения вторых производных, получим уравнение относительно неизвестных y_i‘ (i=2, 3, 4, …, n-1):

Совокупность уравнений (2) для каждой внутренней узловой точки (i=2, 3, 4, …, n-1) образует трехдиагональную систему линейных уравнений. При этом считается, что значения первых производных E₁ и Е_N соответственно в первой х₁ и последней х_N точках известны.

Добавляя два граничных условия y₁‘=E₁ и у_N‘=Е_N, переходим к системе n уравнений, которые могут быть решены относительно первых производных в узловых точках.

Для решения трехдиагональной системы n-линейных уравнений используется эффективный алгоритм, который называется методом прогонки. Метод прогонки является наиболее важным частным случаем метода Гаусса и применяется для систем линейных уравнений с трехдиагональной матрицей:

Где a_i, b_i, c_i — коэффициенты линейного уравнения.

Отсюда определяем x_i через x_i+1:

Уменьшив индекс в формуле (4) на единицу и подставив в уравнение (3), получим:

Чтобы выражение (5) совпало с (4), необходимо равенство дробей правой части (5) соответственно ξ_i+1 и η_i+1. Отсюда получаем выражения для определения коэффициентов при прямом ходе:

В результате решения методом прогонки получим вектор первых производныхy_i‘ (i=1, 2, …, n) в узловых точках сплайна. Значения функции сплайна внутри каждого отрезка (x_i-1, x_i) определяются из многочлена (1), коэффициенты которого вычисляются в соответствии с равенством (2), т. е.