Разделение граничной линии стекла на три участка производится условно и зависит в основном от размерных цепочек чертежа. Число узловых точек на участках может быть различным.
Расчетным путем проводится единое упорядочение исходных узловых точек и рассчитываются их абсолютные координаты, которые объединяются в двух результирующих векторах.
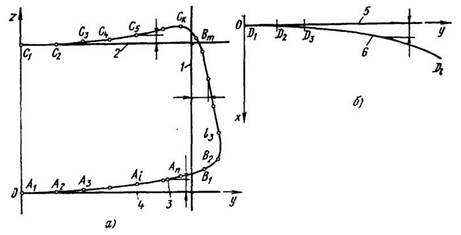
Рис. 9. Система координат и исходные точки: а — граничной линии; б — линии средней кривизны ветрового стекла; 1 — база боковой кромки; 2 — база верхней кромки; 3 — фронтальная проекция линии кромок стекла; 4 — база нижней кромки; 5 — база линии кривизны; 6 — линии средней кривизны.
Для перехода к пространственному описанию поверхности ветрового стекла используется вторая проекция, связанная с кривизной стекла. Исходя из принятых допущений, в качестве исходной принимается проекция средней линии кривизны. Узловые точки и система координат средней линии кривизны ветрового стекла представлены также на рис. 9.
Точки линии кривизны (D1, D2, …, Dl) упорядочены слева направо, абсциссы их задаются в приращениях относительно предыдущих точек (первая имеет нулевую абсциссу).
Координатная система (xyz), оси которой представлены на рис. 9, соответствует вертикальному ветровому стеклу и не зависит от расположения стекла на автомобиле. Такое функциональное выделение геометрических характеристик ветрового стекла позволяет значительно упростить подготовку исходных данных и производить ее по типовой схеме без учета наклона ветрового стекла на автомобиле.
Исходные узловые точки граничной линии ветрового стекла образуют табличную функцию zi=f(yi) (где i= 1, 2, …, s), которая не является однозначной. Сплайн-функция может быть построена только для однозначной функции с упорядоченной монотонно возрастающей последовательностью значений аргумента. Поэтому используется параметрическое задание функции, для чего вводится новая независимая переменная t, удовлетворяющая указанным выше требованиям. Вычисляются сплайн-приближения для z=f1(t) и y=f2(t). Точки yj, zj искомого сплайна соответствуют параметру tj.